Centrioles Go for a Stroll
We do not grow absolutely, chronologically. We grow sometimes in one dimension, and not in another; unevenly.
We grow partially. We are relative. We are mature in one realm, childish in another.
The past, present, and future mingle and pull us backward, forward, or fix us in the present.
We are made up of layers, cells, constellations.
- Anais Nin
Cells let us walk, talk, think, make love and realise the bath water is cold.
- Lorraine Lee Cudmore
 by Manfred Schliwa by Manfred Schliwa
Centrioles are arguably the most enigmatic cell organelles.
In most animal cells, a pair of centrioles resides in the centrosome - a macromolecular complex that organises the microtubule system (part of the cell's internal skeleton). The two
centrioles, a mother and a daughter, "are positioned at right angles to each other." This quote from a popular textbook epitomises the idea of a fixed arrangement of the two bodies within the
centrosome (see figure 1, an end-on view of one of the centrioles, while at the bottom is a longitudinal view of the other centriole).
 Deviations from a close apposition are considered exceptional. Not so, say Matthieu Piel and colleagues (J.
Cell Biol. 149, 317-330; 2000). They have been following the behaviour of centrioles throughout the cell cycle (the time between successive cell divisions) in living cells. Deviations from a close apposition are considered exceptional. Not so, say Matthieu Piel and colleagues (J.
Cell Biol. 149, 317-330; 2000). They have been following the behaviour of centrioles throughout the cell cycle (the time between successive cell divisions) in living cells.
Centrioles are difficult to see by standard light microscopy, so Piel et al made use of the fluorescent tag green fluorescent protein (GFP). They fused GFP to centrin, a small
calcium-binding protein present in the lumen of the centriole. Fluorescence - a marker of the amount of GFP-tagged centrin - is always more intense in the mother centriole. So, the
intensity of fluorescence seems to be indicative of the maturity of a centriole. This allowed the authors to show that a daughter centriole remains "immature" until it duplicates and itself
becomes a mother.
The observation also indicates that one centriole may not be able to replace the other functionally, but this needs to be confirmed.
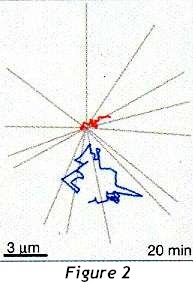
 The most striking observation, however, is that the two centrioles exhibit dramatically different
behaviour. For several hours after cell division, the daughter centriole roams extensively through the body of the cell, separating from the mother by many micrometres. Motility gradually
subsides at the time of centriole duplication, the start of which coincides with the beginning of DNA replication in the nucleus. But these movements also take place - and are more
pronounced - in the absence of nuclei. The most striking observation, however, is that the two centrioles exhibit dramatically different
behaviour. For several hours after cell division, the daughter centriole roams extensively through the body of the cell, separating from the mother by many micrometres. Motility gradually
subsides at the time of centriole duplication, the start of which coincides with the beginning of DNA replication in the nucleus. But these movements also take place - and are more
pronounced - in the absence of nuclei.
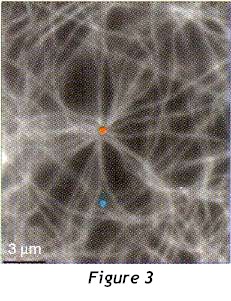
An example of these movements over a period of 20 minutes is shown in figure 2. While the daughter (blue) runs free, the mother centriole (red) resides in the centre of the microtubule array
(see figure 3).
Splitting of the centriole pair has previously been observed under certain experimental conditions or in specialised cell types, but what the work of Piel et al implies is
that centriolar excursions are a normal event during a considerable portion of the cell cycle. Why one centriole should roam the cell after completion of cell division is
unknown, as is the mechanism underpinning these movements. But the observations shake the myth of a stereotypical, right-angled orientation of centrioles, and suggest that
these curious organelles might have some hitherto unsuspected functions associated with their wanderings.
Manfred Schliwa is at the Institute for Cell Biology, University of Munich, Schillerstrasse 42, 80336 Munich, Germany. e-mail:
schliwa@bio.med.uni-muenchen.de
Source: Nature Vol 405 18 May 2000

New Telomere Discovery Could Help Explain Why Cancer Cells Never Stop Dividing
by Joachim Lingner
|
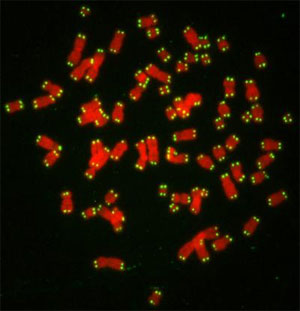
A human metaphase stained for telomeric repeats. DAPI stained chromosomes are false-coloured in red, telomeres are in green.
|
Lausanne, Switzerland, October 4, 2007 – A group working at the Swiss Institute for Experimental Cancer Research (ISREC) in collaboration with the University of Pavia
has discovered that telomeres, the repeated DNA-protein complexes at the end of chromosomes that progressively shorten every time a cell divides, also contain RNA. This
discovery, published online October 4 in Science Express, calls into question our understanding of how telomeres function, and may provide a new avenue of attack for
stopping telomere renewal in cancer cells.
Inside the cell nucleus, all our genetic information is located on twisted, double stranded molecules of DNA which are packaged into chromosomes. At the end of these
chromosomes are telomeres, zones of repeated chains of DNA that are often compared to the plastic tips on shoelaces because they prevent chromosomes from fraying, and thus
genetic information from getting scrambled when cells divide. The telomere is like a cellular clock, because every time a cell divides, the telomere shortens. After a cell has
grown and divided a few dozen times, the telomeres turn on an alarm system that prevents further division. If this clock doesn’t function right, cells either end up with
damaged chromosomes or they become “immortal” and continue dividing endlessly – either way it’s bad news and leads to cancer or disease. Understanding how telomeres function,
and how this function can potentially be manipulated, is thus extremely important.
The DNA in the chromosome acts like a sort of instruction manual for the cell. Genetic information is transcribed into segments of RNA that then go out into the cell and
carry out a variety of tasks such as making proteins, catalyzing chemical reactions, or fulfilling structural roles. It was thought that telomeres were “silent” – that their
DNA was not transcribed into strands of RNA. The researchers have turned this theory on its head by discovering telomeric RNA and showing that this RNA is transcribed from DNA
on the telomere.
Why is this important" In embryonic cells (and some stem cells), an enzyme called telomerase rebuilds the telomere so that the cells can keep dividing. Over time, this
telomerase dwindles and eventually the telomere shortens and the cell becomes inactive. In cancer cells, the telomerase enzyme keeps rebuilding telomeres long past the cell’s
normal lifetime. The cells become “immortal”, endlessly dividing, resulting in a tumor. Researchers estimate that telomere maintenance activity occurs in about 90% of human
cancers. But the mechanism by which this maintenance takes place is not well understood. The researchers discovered that the RNA in the telomere is regulated by a protein in
the telomerase enzyme. Their discovery may thus uncover key elements of telomere function.
“It’s too early to give yet a definitive answer,” to whether this could lead to new cancer therapies, notes Joachim Lingner, senior author on the paper. “But the
experiments published in the paper suggest that telomeric RNA may provide a new target to attack telomere function in cancer cells to stop their growth.”
Joachim Lingner is an Associate Professor at the EPFL (Ecole Polytechnique Fédérale de Lausanne). Funding for this research was provided in part by the Swiss National
Science Foundation NCCR “Frontiers in Genetics”.
Source: eurekalert.org “Telomeric Repeat Containing RNA and RNA Surveillance
Factors at Mammalian Chromosome Ends” 4 October 2007 photo credit Claus Azzalin, ISREC

Interest in Consciousness Research & Personal Statement
by Stuart Roy Hameroff
I divide my professional time at the University of Arizona between:
- Practicing and teaching clinical anæsthesiology in the surgical operating rooms at University Medical Center, and
- Research into the mechanism of consciousness.
My interests in the nature of mind began during my undergraduate days at the University of Pittsburgh in the late 60's, where I studied mostly chemistry, physics and
mathematics. Later, during medical school at Hahnemann Medical College in Philadelphia I spent a summer research elective in the laboratory of hæmatologist/oncologist Dr Ben
Kahn. While studying mitosis (cell division) in white blood cells under the microscope I became fascinated by the mechanical movements of tiny organelles (centrioles) and
delicate threads which teased apart chromosomes and established cell shape and architecture. These mitotic spindles were called microtubules, cylindrical protein
assemblies. I began to wonder how these microtubules were guided and organised - could there be some kind of intelligence, or computation at that level? The microtubules
were actually lattices of individual proteins called tubulin, and the crystal-like arrangement of tubulins to make up microtubules reminded me of a computer switching
circuit. Could microtubules be processing information like a computer?
At just about that time (early 1970's) the fine structure of living cells was being appreciated fully for the first time. It seems that the fixative agent for electron
microscopy (osmium tetroxide) had for 30 years been destroying much of the internal structure, suggesting cells were merely membrane-bound bags of soup. A new fixative
(glutaraldehyde) began to reveal that cell interiors were complex scaffoldings of interconnected proteins collectively called the cytoskeleton, whose main components were the seemingly
intelligent microtubules. Neurons, it turned out, were loaded with microtubules which were cross connected by linking proteins to form complex networks. I began to wonder if the
abundance of microtubules in neurons was relevant to the problem of consciousness.
After medical school and internship in Tucson, Arizona I considered specialising in neurology or psychiatry to research the brain/mind problem. But the chairman of the
Department of Anæsthesiology at the University of Arizona, Professor Burnell Brown convinced me that understanding the precise molecular mechanism of general anaesthetic gases was the
most direct path toward unlocking the enigma of consciousness. He also gave me a paper showing that the anæsthetics caused microtubules to disassemble. I became an
anæsthesiologist and joined Burnell's faculty in 1977 after my residency training. I researched a number of areas in anæsthesiology but eventually focused on my primary
interests: consciousness, anæsthetic mechanisms and cytoskeletal microtubules. Sadly, Burnell died several years ago. I miss him, and am grateful to him for my career.
During the 1980's I published a number of papers and one book (Ultimate Computing-Biomolecular Consciousness and Nanotechnology, Elsevier-North Holland, Amsterdam, 1987) on
models of information processing in microtubules. But even if microtubules were actually computers, critics said, how would that explain the problem of consciousness?
In the early 1990's the study of consciousness became increasingly popular and I was strongly influenced by Roger Penrose's The Emperor's New Mind (and later Shadows of
the Mind, Oxford Press, 1989 and 1994). Quite famous for his work in relativity, black holes, and quantum mechanics, Roger had turned to the problem of consciousness and
concluded the mind was more than complex computation. Something else was necessary, and that something, he suggested, was a particular type of quantum computation he was
proposing ("objective reduction" - a self-collapse of the quantum wave function due to quantum gravity). He was linking consciousness to a basic process in underlying
spacetime geometry - reality itself! It seemed fascinating and plausible to me, but Roger didn't have a good candidate biological site for his proposed process. I thought,
could microtubules be quantum computers? I wrote to him, and we soon met in his office in Oxford in September 1992. Roger was struck by the mathematical symmetry and beauty
of the microtubule lattice and thought it was the optimal candidate for his proposed mechanism. Over the next few years through discussions at conferences in Sweden, Tucson,
Copenhagen and elsewhere, and a memorable hike through the Grand Canyon in 1994, we began to develop a model for consciousness involving Roger's objective reduction occurring in
microtubules within the brain's neurons. Because the proposed microtubule quantum states were "tuned" by linking proteins, we called the process "orchestrated objective
reduction."
In December 1997 the Fetzer Institute awarded our group $1.4 million to continue our efforts in Consciousness Studies, and to build a Center for Consciousness Studies at the
University of Arizona. In May 1998 the first 10 recipients of Fetzer research grants for $20,000 administered through our Center were announced. The awards will occur again
in 1999 and 2000. In July 1998 we initiated an email discussion group devoted to quantum approaches to consciousness: Quantum-Mind.
Since that time the debate over the role of significant quantum mechanisms in the brain has become heated, with mainstream scientists attempting to disprove and silence quantum
claims. Despite apparent problems with decoherence at brain temperature I remain convinced that nature has evolved mechanisms to support a quantum role in
consciousness. Scott Hagan, Jack Tuszynski and I have been working on the decoherence problem and feel we have a solution.
Source: Taken from one of Stuart Hameroff's now-defunct websites.

The Sum of the Parts: Add the Limits of Computation
to the Age of the Universe and What Do You Get?
A Radical Take on the Emergence of Life
by Paul Davies
Take a bucketful of subatomic particles. Put them together one way, and you get a baby. Put them together another way and you'll get a rock. Put
them together a third way and you'll get one of the most surprising materials in existence: a high-temperature superconductor. How can such
radically different properties emerge from different combinations of the same basic matter?
The history of science is replete with investigations of the unexpected qualities that can arise in complex systems. Shoals of fish and ant
colonies seem to display a collective behaviour that one would not predict from examining the behaviour of a single fish or ant. High-temperature
superconductors and hurricanes offer two more examples where the whole seems to be greater than the sum of its parts. What is still hotly disputed is
whether all such behaviour can ultimately be derived from the known laws of physics applied to the individual constituents, or whether it represents the
manifestation of something genuinely new and different - something that, as yet, we know almost nothing about. A new factor could shed light on this most
fundamental question. And it comes from an entirely unexpected quarter: cosmology.
The standard scientific view, known as reductionism, says that everything can ultimately be explained in terms of the "bottom level" laws of physics. Take
the origin of life. If you could factor in everything about the prebiotic soup and its environment - and assuming you have a big enough computer
- you could in principle predict life from the laws of atomic physics, claim the reductionists.
What has become increasingly clear, however, is that many complex systems are computationally intractable. To be sure, their evolution might be
determined by the behaviour of their components, but predictive calculations are exponentially hard. The best that one can do is to watch and see how they
evolve. Such systems are said to exhibit "weak emergence".
But a handful of scientists want to go beyond this, claiming that some complex systems may be understood only by taking into account additional laws or
"organising principles" that emerge at various levels of complexity. This point of view is called "strong emergence", and it is anathema to reductionists.
The debate is often cast in the language of "Laplace's demon." Two centuries ago, Pierre Laplace pointed out that if a superintelligent demon knew
at one instant the position and motion of every particle in the universe, and the forces acting between them, the demon could do a massive calculation and
predict the future in every detail, including the emergence of life and the behaviour of every human being. This startling conclusion remains an
unstated act of faith among many scientists, and underpins the case for reductionism.
Laplace's argument contains, however, a questionable assumption: the demon must have unlimited computational power. Is this reasonable? In
recent years, there has been intense research into the physical basis of digital computation, partly spurred by efforts to build a quantum computer. The
late Rolf Landauer of IBM, who was a pioneer of this field, stressed that all computation must have a physical basis and therefore be subject to two
fundamental limitations. The first is imposed by the laws of physics. The second is imposed by the resources available in the real universe.
The fundamental piece of information is the bit. In standard binary arithmetic of the sort computers use, a bit is simply a 1 or a 0. The most
basic operation of information processing is a bit-flip: changing a 1 to a 0 or vice versa. Landauer showed that the laws of physics impose limits on the
choreography of bit-flips in three ways. The first is Heisenberg's uncertainty principle of quantum mechanics, which defines a minimum time needed
to process a given amount of energy. The second is the finite speed of light, which restricts the rate at which information can be shunted from place
to place. The third limit comes from thermodynamics, which treats entropy as the flip side of information. This means a physical system cannot store
more bits of information in its memory than is allowed by its total entropy.
Given that any attempt to analyse the universe and its processes must be subject to these fundamental limitations, how does that affect the performance
of Laplace's demon? Not at all if the universe possesses infinite time and resources: the limitations imposed by physics could be compensated for simply by
commandeering more of the universe to analyse the data. But the real universe is not infinite, at least not in the above sense. It originated
in a big bang 13.7 billion years ago, which means light can have travelled at most 13.7 billion light years since the beginning. Cosmologists express
this restriction by saying that there is a horizon in space 13.7 billion light years away. Because nothing can exceed the speed of light, regions of
space separated by more than this distance cannot be in causal contact: what happens in one region cannot affect the other. This means the demon would
have to make do with the resources available within the horizon.
Seth Lloyd of the Massachusetts Institute of Technology recently framed the issue like this. Suppose the entire universe (within the effective
horizon) is a computer: how many bits could it process in the age of the universe? The answer he arrived at after applying Landauer's limits is 10120
bits. That defines the maximum available processing power. Any calculation requiring more than 10120 bits is simply a fantasy,
because the entire universe could not carry it out in the time available.
Lloyd's number, vast though it is, defines a fundamental limit on the application of physical law. Landauer put it this way: "a sensible theory
of physics must respect these limitations, and should not invoke calculative routines that in fact cannot be carried out". In other words, Landauer and
Lloyd have discovered a fundamental limit to the precision of physics: we have no justification in claiming that a law must apply - now, or at any earlier time
in the universe's existence - unless its computational requirements lie within this limit, for even a demon who commandeered the entire cosmos to compute could
not achieve predictive precision beyond this limit. The inherent fuzziness that this limit to precision implies is quite distinct from quantum uncertainty,
because it would apply even to deterministic laws.
How does this bear on the question of strong emergence - the idea that there are organising principles that come into play beyond a certain threshold of
complexity? The Landauer-Lloyd limit does not prove that such principles must exist, but it disproves the long-standing claim by reductionists that they
can't. If the micro-laws - the laws of physics as we know them - cannot completely determine the future states and properties of some physical systems,
then there are gaps left in which higher-level emergent laws can operate.
So is there any way to tell if there is some substance to the strong-emergentists' claims? For almost all systems, the Landauer-Lloyd limit is nowhere near
restrictive enough to make any difference to the conventional application of physical laws. But certain complex systems exceed the limit. If
there are emergent principles at work in nature, it is to such complex systems that we should look for evidence of their effects.
A prime example is living organisms. Consider the problem of predicting the onset of life in a prebiotic soup. A simple-minded approach is to
enumerate all the possible combinations and configurations of the basic organic building blocks, and calculate their properties to discover which would be
biologically efficacious and which would not.
Calculations of this sort are already familiar to origin-of-life researchers. There is considerable uncertainty over the numbers, but it scarcely matters
because they are so stupendously huge. For example, a typical small protein is a chain molecule made up of about 100 amino acids of 20 varieties. The
total number of possible combinations is about 10130, and we must multiply this by the number of possible shapes the molecule can take, because
its shape affects its function. This boosts the answer to about 10200, already far in excess of the Landauer-Lloyd limit, and shows how the remorseless
arithmetic of combinatorial calculations makes the answers shoot through the roof with even modest numbers of components.
The foregoing calculation is an overestimate because there may be many other combinations of amino acids that exhibit biological usefulness - it's hard to
know. But a plausible guesstimate is that a molecule containing somewhere between 60 and 100 amino acids would possess qualities that almost certainly
couldn't have been divined in the age of the universe by any demon or computer, even with all the resources of the universe at its disposal. In other
words, the properties of such a chain simply could not - even in principle - be traced back to a reductionist explanation.
Strikingly, small proteins possess between 60 and 100 amino acids. The concordance between these two sets of numbers, one derived from theoretical
physics and cosmology, the other from experimental biology, is remarkable. A similar calculation for nucleotides indicates that in DNA, the properties of
strings of more than about 200 base pairs might require additional organising principles to explain their properties. Since genes have upwards of about
this number of base pairs, the inference is clear: emergent laws may indeed have played a part in giving proteins and genes their functionality.
Biologists such as Christian de Duve have long argued that life is "a cosmic imperative", written into the laws of nature, and will emerge inevitably and
naturally under the right conditions. However, they have never managed to point to the all-important laws that make the emergence of life "law-like". It
seems clear from the Landauer-Lloyd analysis that the known laws of physics won't bring life into existence with any inevitability - they don't have life
written into them. But if there are higher-level, emergent laws at work, then biologists like de Duve may be right after all - life may indeed be written
into the laws of nature. These laws, however, are not the bottom-level laws of physics found in the textbooks.
And while we are looking for phenomena that have long defied explanation by reductionist arguments, what about the emergence of familiar reality - what
physicists call "the classical world" - from its basis in quantum mechanics? For several decades physicists have argued about how the weird and shadowy
quantum micro-world interfaces with the concrete reality of the classical macro-world. The problem is that a quantum state is generally an amalgam
of many alternative realities, coexisting in ghostly superposition. The macro-world presented to our senses is a single reality. How does the
latter emerge from the former?
There have been many suggestions that something springs into play and projects out one reality from many. The ideas for this "something" range
from invoking the effect of the observer's mind to the influence of gravitation. It seems clear, however, that size or mass are not relevant variables because
there are quantum systems that can extend to everyday dimensions: for example, superconductors.
One possible answer is that complexity is the key variable. Could it be that a quantum system becomes classical when it is complex enough for emergent
principles to augment the laws of quantum mechanics, thereby bringing about the all-important projection event?
To find where, on the spectrum from atom to brain, this threshold of complexity might lie, we can apply the Landauer-Lloyd limit to quantum states of
various configurations. One such complex state, known as an entanglement, consists of a collection of particles like electrons with spins directed either
up or down, and linked together in a quantum superposition. Entangled states of this variety are being intensively studied for their potential role in
quantum computation. The number of up-down combinations grows exponentially with the number of electrons, so that by the time one has about
400 particles the superposition has more components than the Landauer-Lloyd limit. This suggests that the transition from quantum to classical might
occur, at least in spin-entangled states, at about 400 particles. Though this is beyond current technology, future experiments could test the idea.
For 400 years, a deep dualism has lain at the heart of science. On the one hand the laws of physics are usually considered universal, absolute and
eternal: for example, a force of 2 newtons acting on a 2-kilogram mass will cause it to accelerate by 1 metre per second per second, wherever and whenever
in the universe the force is applied. On the other hand, there is another factor in our description of the physical world: its states. These are not
fixed in time. All the states of a physical system - whether we are talking about a hydrogen atom, a box full of gas or the recorded prices on the
London stock market - are continually moving and changing in a variety of ways. In our descriptions of how physical systems behave, these states are as
important as the laws. After all, the laws act on the states to predict how the system will behave. A law without a state is like a traffic rule
in a world with no cars: it doesn't have any application.
What the new paradigm suggests is that the laws of physics and the states of the real world might be interwoven at the deepest level. In other words, the
laws of physics do not sit, immutable, above the real world, but are affected by it. That sounds almost heretical, but some physicists - most notably John
Wheeler - have long speculated that the laws of physics might not be fixed "from everlasting to everlasting", to use his quaint expression. Most
cosmologists treat the laws of physics as "given", transcending the physical universe. Wheeler, however, insisted the laws are "mutable" and in some
manner "congeal" into their present form as the universe expands from an initial infinitely dense state. In other words, the laws of physics might emerge
continuously from the ferment of the hot big bang.
It seems Wheeler's ideas and the Landauer-Lloyd limit point in the same direction. And that means the entire theory of the very early universe
could be back in the melting pot.
Paul Davies is at the Australian Centre for Astrobiology at Macquarie University, Sydney
Source: New Scientist 5 March 2005 page 34 from "Emergent biological principles and the computational resources of the universe", Complexity (vol 10 (2), p 1)

For articles on bacteria, centrioles, chairs, nebulae, asteroids, robots, memory, chirality, pain, fractals, DNA, geology, strange facts, extra dimensions, spare parts,
discoveries, ageing and more click the "Up" button below to take you to the Table of Contents for this Science section.
|  Animals
Animals Animation
Animation Art of Playing Cards
Art of Playing Cards Drugs
Drugs Education
Education Environment
Environment Flying
Flying History
History Humour
Humour Immigration
Immigration Info/Tech
Info/Tech Intellectual/Entertaining
Intellectual/Entertaining Lifestyles
Lifestyles Men
Men Money/Politics/Law
Money/Politics/Law New Jersey
New Jersey Odds and Oddities
Odds and Oddities Older & Under
Older & Under Photography
Photography Prisons
Prisons Relationships
Relationships Science
Science Social/Cultural
Social/Cultural Terrorism
Terrorism Wellington
Wellington Working
Working Zero Return Investment
Zero Return Investment by Manfred Schliwa
by Manfred Schliwa Deviations from a close apposition are considered exceptional. Not so, say Matthieu Piel and colleagues (J.
Cell Biol. 149, 317-330; 2000). They have been following the behaviour of centrioles throughout the cell cycle (the time between successive cell divisions) in living cells.
Deviations from a close apposition are considered exceptional. Not so, say Matthieu Piel and colleagues (J.
Cell Biol. 149, 317-330; 2000). They have been following the behaviour of centrioles throughout the cell cycle (the time between successive cell divisions) in living cells. The most striking observation, however, is that the two centrioles exhibit dramatically different
behaviour. For several hours after cell division, the daughter centriole roams extensively through the body of the cell, separating from the mother by many micrometres. Motility gradually
subsides at the time of centriole duplication, the start of which coincides with the beginning of DNA replication in the nucleus. But these movements also take place - and are more
pronounced - in the absence of nuclei.
The most striking observation, however, is that the two centrioles exhibit dramatically different
behaviour. For several hours after cell division, the daughter centriole roams extensively through the body of the cell, separating from the mother by many micrometres. Motility gradually
subsides at the time of centriole duplication, the start of which coincides with the beginning of DNA replication in the nucleus. But these movements also take place - and are more
pronounced - in the absence of nuclei.